友友们,今天来填一下语言的坑d(ŐдŐ๑),讲一下数组这个东东。
数组的概念
从字面意思上理解,数组就是一堆数据的组合,实际上也确实如此,但又多了一些细节。同一数组中存储的数必须满足以下两个条件:
1.这些数的类型必须相同。
2.这些数在内存中必须是连续存储的。(所谓连续储存,是指数组之中的数据是连续储存的,其地址是连续的)
1 | int a[5]; |
它表示定义了一个整型数组,数组名为 a,定义的数组称为数组 a。此时数组 a 中有 5 个元素,每个元素都是 int 型变量,而且它们在内存中的地址是连续分配的。也就是说,int 型变量占 4 字节的内存空间,那么 5 个int型变量就占 20 字节的内存空间,而且它们的地址是连续分配的。
注意,数组名 a 除了表示该数组之外,还表示该数组的首地址,也就是说,当你使用数组时,实际上是计算机根据数组名到达第n个数据的地址并读出数据,所以读取数组中元素这个操作是一个常数操作(这里不理解也没关系)。
数组的遍历
对数组进行遍历时最常用的操作,即把数组从头到尾的读取一遍,具体操纵一般用循环结构进行操作。
1 | for(int i=0;i<=4;i++) |
上面这个操作就是把数组中所有的元素都变成0,是初始化数组的一种方法。观察上码可以发现,数组中第一个值是a[0]而不是a[1],所以数组a的5个元素分别是a[0],a[1],a[2],a[3],a[4]。
二维数组
1 | int b[2][3] |
上面几个例子都是举了一维数组的例子,现在说说二维数组。有些人习惯于把一维数组看作一条线,而二维便是一个面,比如b数组就是一个2*3的表格,这样虽然也有助于理解二维数组,但不够接近本质。
上面说过,数组的地址是连续的,也就是说其地址就相当于一条连续的线,这样来看的话上面这种解释就出现问题了,下面说一下我自已更喜欢的一种理解:
数组的元素可以是任意类型,那么就让数组作为数组的元素,实现数组的嵌套就能完美解释多维数组了。拿b来说明,它可以看作是由两个元素组成,每个元素则都是一个由三个数据组成的数组
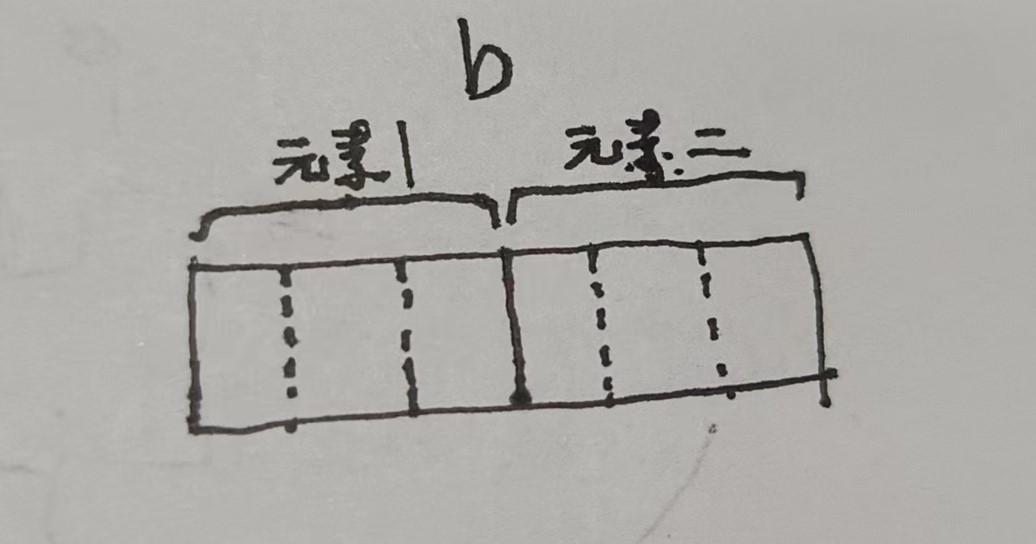
如上图,至于三维四维数组则都是同理了。
好了,今天就到这里了。

